- 目的変数がない、入力データそのものに注目
- データの中に部分集合を見つけたり、データを変換して別の形式で表現したりすることでデータの解釈性を高める
- データに潜むパターンや示唆を見出すために用いる
- 教師なし学習モデルはクラスタリング、次元削減に大別できる
OSEMN (オーサム) Process
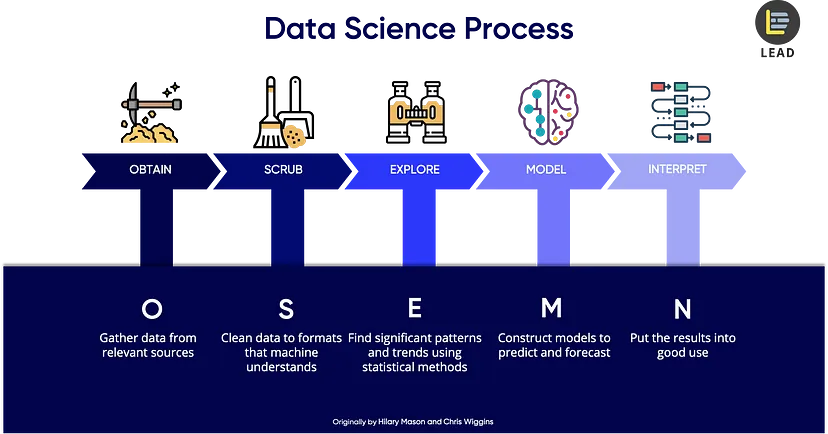
5 Steps of a Data Science Project Lifecycle
データを取得する。データは主にデータベース、CSV, Web APIから取得できる
データを解釈するために整理する。
データには欠損値や、モデルに使用できない型になっているデータが存在する。また、(リレーショナル)データベースでは複数のテーブルが混在しており、データ分析がしにくい。列を分割、あるいは結合する必要がある。
pythonでは主にpandasを使う。
モデルに使うためのデータを探す。機械なし学習はここで役立つ。またpythonでは、matplotlibを用いてデータの可視化も行う。
ここではデータのメタ的な理解が必要。そのための探索、特徴量エンジニアリングを行う。
将来を予測するために教師あり学習を用いて機械学習モデルを作る。
データを利用して価値を創出する。(稼ぐ)
PCA: Principal Component Analysis (主成分分析)
より少ない特徴量でデータを理解するための手法。多変数データを特徴を保ちながら少変数で表現すること。
機械学習において、特徴量は多すぎないほうが良い。データの解釈性を失う恐れがあるし、過学習が起こりやすい。さらに、処理スピードも遅くなる。それらを解決するために「特徴量を減らす=次元削減をする」
変数間に相関のあるデータに対して有効。代表的な次元削減の手法。
元データの変数から新たな変数を構成する。
たいていの場合3次元以内に収める
以下のサイトで視覚的に理解できる
Principal Component Analysis explained visually

主成分における内積の分散が最大となるような主成分軸を見つける→基底変換
→基底を変換したいので変換行列が必要、最適な変換行列を求める

i番目のp次元ベクトルxi∗が(xi1,xi2,...,xip)Tのとき データXを、X=x11x21⋮xn1x12x22⋮xn2......⋱...x1px2p⋮xnp,p次元からq次元に変換する変換行列をw=w11w21⋮wp1w12w22⋮wp2......⋱...w1qw2q⋮wpqとする。 Tip
変換行列のそれぞれの列は基底ベクトルを表す
このとき、圧縮されたデータをYとすると、Y=Xwが成り立つ。次に、射影後のベクトルについて考える。 元のデータベクトルxi∗を求めたい主成分の方向に射影した結果をyi、この時の主成分をw=(w1,w2,...,wp)Tとすると、yi=wTxi∗と表せる。 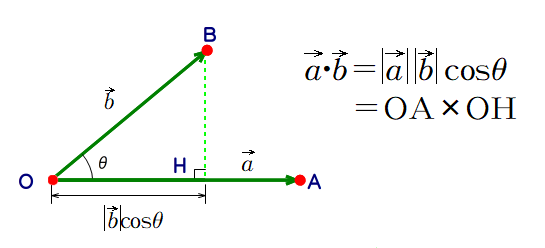
Tip
ベクトルの方向が近ければ近いほど、内積は大きくなる。その分内積の値のズレも大きくなる→その方向における内積の分散の最大値を求めれば主成分が決まるのでは?
このとき、分散s2=n1i=1∑n(yi−y)2,平均y=n1i=1∑nyi=w1x∗1+w2x∗2+...+wpx∗p=wT(x∗1,x∗2,...,x∗p)となるので、s2=n1i=1∑n(wT(xi1,xi2,...,xip)−wT(x∗1,x∗2,...,x∗p))2=n1i=1∑n⎩⎨⎧wxi1−x∗1xi2−x∗2⋮xip−x∗p⎭⎬⎫2=n1i=1∑nwTxi1−x∗1xi2−x∗2⋮xip−x∗pxi1−x∗1xi2−x∗2⋮xip−x∗pTw=wTn1i=1∑nxi1−x∗1xi2−x∗2⋮xip−x∗pxi1−x∗1xi2−x∗2⋮xip−x∗pTw=wTSw※共分散行列S=s11s21⋮sp1s12s22⋮sp2......⋱...s1ps2p⋮spp,sjk=n1i=1∑n(xij−x∗j)(xik−x∗k) ここでs2=wTSw(wTw=1)が最大値を取るときのwをラグランジュの未定乗数法で求める。f(w)=s2=wTSw,制約:g(w)=wTw−1=0のもとで、ラグランジュ関数はF(w,λ)=f(w)+λg(w)となる。(wはいくらでも大きくできてしまうので制約が必要) ラグランジュの未定乗数法と例題 | 高校数学の美しい物語
s2が最大化するとき∂w∂F(w,λ)=2Sw−2λw=0より、Sw=λw Sw=λwは共分散行列の固有方程式を表している。ちなみに両辺にwTをかけると、wTSw=wTλw,式変形していくと仮定よりwTSw=λwTw=λ=s2 したがって固有値λは分散そのものを表す。また、それぞれに対する固有ベクトルwは変換後の基底=主成分であり、求めたい変換行列wは(w1w2...wq)となる。 各成分ごとに計算される固有値を固有値の総和で割ると、主成分の重要度の割合で表現することができる。この時の割合を寄付率といい、各主成分がデータをどれぐらい説明しているかを表現している。
第k主成分の寄付率=∑i=1nλiλk
次に示すプログラムは、RandomStateオブジェクトを使って、2変数のデータセットを生成し、各変数について標準化したものをプロットしたものである。
from sklearn.preprocessing import StandardScaler
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
sample = np.random.RandomState(1)
X = np.dot(sample.rand(2, 2), sample.randn(2, 200)).T
sc = StandardScaler()
X_std = sc.fit_transform(X)
print('相関係数{:.3f}:'.format(sp.stats.pearsonr(X_std[:, 0], X_std[:, 1])[0]))
plt.scatter(X_std[:, 0], X_std[:, 1])
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_std)
変換行列(固有ベクトル)を出力する
分散(固有値)を出力する
print('各主成分の分散:{}'.format(pca.explained_variance_))
arrowprops=dict(arrowstyle='->',
linewidth=2,
shrinkA=0, shrinkB=0)
def draw_vector(v0, v1):
plt.gca().annotate('', v1, v0, arrowprops=arrowprops)
plt.scatter(X_std[:, 0], X_std[:, 1], alpha=0.2)
for length, vector in zip(pca.explained_variance_, pca.components_):
v = vector * 3 * np.sqrt(length)
draw_vector(pca.mean_, pca.mean_ + v)
plt.axis('equal')
from sklearn.datasets import load_breast_cancer
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
%matplotlib inline
cancer = load_breast_cancer()
cancer
df = pd.DataFrame(cancer.data, columns=cancer.feature_names)
df["target"] = cancer.target
df
欠損値などはありませんでした。
malignant = df[df["target"] == 0]
benign = df[df["target"] == 1]
fig, axes = plt.subplots(6,5,figsize=(20,20))
ax = axes.ravel()
for i, column in enumerate(df.columns[:-1]):
_,bins = np.histogram(df[column], bins=50)
ax[i].hist(malignant[column], bins, alpha=.5)
ax[i].hist(benign[column], bins, alpha=.5)
ax[i].set_title(column)
ax[i].set_yticks(())
ax[0].set_ylabel('Count')
ax[0].legend(['malignant','benign'],loc='best')
fig.tight_layout()
しかし特徴的なデータは見当たらないので、主成分分析を用いて次元削減を行ってみる
sc = StandardScaler()
X_std = sc.fit_transform(cancer.data)
pca = PCA(n_components=2)
pca.fit(X_std)
X_pca = pca.transform(X_std)
print('X_pca shape:{}'.format(X_pca.shape))
print('Explained variance ratio:{}'.format(pca.explained_variance_ratio_))
X_pcaは569行2列に変換された→569個の二次元ベクトルの集合
X_pca = pd.DataFrame(X_pca, columns=['pc1','pc2'])
X_pca = pd.concat([X_pca, pd.DataFrame(cancer.target, columns=['target'])], axis=1)
pca_malignant = X_pca[X_pca['target']==0]
pca_benign = X_pca[X_pca['target']==1]
ax = pca_malignant.plot.scatter(x='pc1', y='pc2', color='red', label='malignant');
pca_benign.plot.scatter(x='pc1', y='pc2', color='blue', label='benign', ax=ax);
x = np.arange(-5, 9)
y = 1.7 * x - 0.8
ax.plot(x, y, color="black")
境界線はSVMを使うとより最適化できるかも
累計寄付率を求めてみると、次元が大きくなるほど値は変化しなくなる。なくなるぐらいの次元がベスト。逆に次元が大きくなるほど累計寄付率が大きく変わる場合、それは相関関係があるとは言えない。PCRを使ってもあまり意味がない。
主成分分析を用いて得られる結果は、統計的な指標や数値情報である。しかし、見つかった主成分が具体的にどのような意味を持つのかは、分析者の解釈に委ねられ、直感的には理解しづらい場合がある。その理由は、主成分自体が元のデータと直接の関連を持たないためである。
主成分分析は、データが正規分布に従っているという仮定の元に成り立っている分析手法である。正規分布とは、平均値の周りにデータが集中し、左右対称の釣鐘状にデータが広がるような分布をさす。正規性の仮定を満たさないデータに主成分分析を適用すると、主成分の方向や寄与率が歪められる可能性がある。
外れ値は通常のデータパターンから大きく逸脱した値であり、分析結果に悪影響を及ぼす可能性がある。主成分分析はデータの分散を最大化する方向を求める手法である。そのため、外れ値が分散に大きく影響すると、主成分の方向や寄与率が歪められてしまう。これにより、分析結果が歪んだり、軸の解釈が困難になってしまう問題が発生する。



